Monte Carlo, Markov Chains, and Detail Balance

17 Dec 2017

Introduction and Motivation

I realized while writing up my post on the Quantum Variational Monte Carlo that there was enough non-physics background information to warrant a separate post. I went back to one of those resources, Hjorth-Jensen’s notes, which a professor of mine had provided as an extra resource and, at the time, I had completely passed over.

It’s too bad that I did because a few chapters I pull from in this post give wonderfully simplistic examples of Monte Carlo simulations, Markov processes, and the motivation behind the detail balance requirement. This post is more or less my notes from those notes. These are general approaches to problems which have probabilistic features, and extend in use cases beyond physics, so it would be good to explain their use before applying them.

TL;DR

Raw Monte Carlo, random importance sampling, is not very useful for even simple cases where methods fail to converge if the acceptances are small. Some Markov Process, a chain of states describing some system and linked by transition matrices, can be introduced to defeat this problem. The nature of the acceptance criteria for random moves between states must abide by both ergodicity and detailed balance constraints; an example which satisfies both being the Metropolis-Hastings algorithm.

Algorithms like this are called Markov chain Monte Carlo methods, MCMC.

Discrete forms for Vector Calculus Operators, a cheat sheet

Because computations are finite, simulations become discrete; continuous functions are represented in a space which is divided into small cells. In other words, the dx which we put at the end of our integrals is no longer infinitesimally small but has some real length (or time, or frequency, etc) value, and our integrals all become really long sums as a result. Below are some common calculus operators as they appear in a discrete 2 dimensional case:

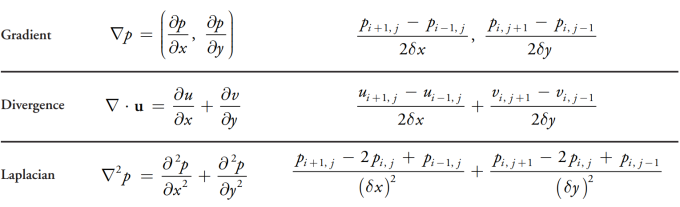
Which I borrowed from a chapter of Nvidias cuda gems book to avoid the Latex work. I promise that thinking about these for a minute to check that they make sense is worth anyone’s time here.

Markov Chains, Discretized Diffusion example

We can apply a Markov chain to random walks simulating the evolution described by the diffusion equation:

$$ \frac{\partial w(x, t)}{\partial t} = D \frac{\partial^2 w(x,t)}{\partial x^2} $$

where

$$ w(x, t)\partial x $$

is the probability of finding a particle in some discrete region dx and at some time t. It is the classical equivalent of the wavefunction I discuss in the variational monte carlo project.

The chain in a Markov chain is a chain between states of a system. The states of our system, for example, can be simply the set of [0, 1] values indicating the position of a particle on a discrete lattice in one dimensional space, with divisions of length $l$

Additionally, we can introduce a probability that the particle will will move right or left by the distance l, Pl, and Pr during some (also discretized) time step $\Delta t = \epsilon$. This can be written:

$$ W_{ij} (\epsilon) = w(il - jl, \epsilon) $$

where:

$$ w(il - jl, \epsilon) = \begin{cases} \frac{1}{2} & \text{if $|i - j| = 1$}  0 & \text{otherwise} \end{cases} $$

The PDF at any later timestep t is generated by applying the transition function w, n times to the state, where n is the number of discrete timesteps to walk through. We can represent the transition in matrix form:

$$ w^n(\epsilon)_{ij} = w(il - jl, n\epsilon) $$

and therefore:

$$ \vec{w}(n\epsilon) = \hat W(\epsilon) \vec{w}(0) $$

Our transition matrix looks like the combination of two matrices which represent right moves $\hat{R}$ and left moves $\hat{L}$ and we apply it to our state with the point at zero:

$$ \begin{pmatrix} 0 & \frac{1}{2} & 0 & 0 & 0 \\\ \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 \\\ 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\\ 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\\ 0 & 0 & 0 & \frac{1}{2} & 0 \\\ \end{pmatrix} $$

This sort transition matrix is sometimes called a Markov matrix, a Probability matrix, or a Stochastic matrix. Note that because all rows and all columns sum to 1 the transition preserves the number of particles in the state. The continued application a Markov matrix forms a Markov chain of states.

Many applications of our transition matrix, written in the Left+Right form:

$$ \hat{w}(\epsilon) = \frac{1}{2}(\hat{L} + \hat{R}) $$
$$ \hat{w}^2(2\epsilon) = \frac{1}{4}(\hat{L}^2 + \hat{R}^2 + 2\hat{R}\hat{L}) $$
$$ \hat{w}^2(3\epsilon) = \frac{1}{8}(\hat{L}^3 + \hat{R}^3 + 3\hat{R}^2\hat{L} + 3\hat{R}\hat{L}^2) $$

or, using binomial coefficients we can represent n timesteps:

$$ \hat{W}^n(n\epsilon) = \frac{1}{2^n}\sum_{k=0}^n {n \choose k} \hat{R}^k\hat{L}^{n-k} $$

Where the 2^n term is a normalization factor. Moving from states i to j:

$$ W(il - jl, n\epsilon) = \begin{cases} \frac{1}{2^n}{n \choose \frac{1}{2}(n + i + j)} & |i - j| \le n \\ 0 & \text{otherwise} \end{cases} $$

Which just says that some probability exists for the particle to be found at a location as long as the location is within the maximum range the particle could have reached by that time. If the particle starts at zero the PDF for locations i becomes:

$$ \hat{w_i}(n\epsilon) = \frac{1}{2^n}{n \choose \frac{1}{2}(n + i)} $$

Converting $i$’s to $xl$’s and $n\epsilon$ to $t$, and using the recursion relation for binomial coefficients:

$$ w(x, t + \epsilon) = \frac{1}{2}w(x + l, t) + \frac{1}{2}w(x - l,t) $$

Which makes sense, the probability to find a particle at position x in the next time step would only be non-zero if there was a particle currently to the right or left. Subtracting w(x, t + e) to get the time derivative on the left side, and multiplying by the proper unit signature:

$$ \frac{w(x, t + \epsilon) - w(x,t)}{\epsilon} = \frac{l^2}{2\epsilon}\frac{w(x + l,t) - 2w(x,t) + w(x - l,t)}{l^2} $$

Looking at the cheat sheet for the gradient and laplacian discrete forms (and removing the extra terms because this is a 1D case) we’ve recovered exactly the discrete form of the diffusion equation from the application of our transition matrix. So, a Markov chain approximates a real physical process given enough states and a small enough time step.

Detailed Balance

Recreating diffusion isn’t all too interesting because the equilibrium state, when our transformation matrix has been applied an “infinite” number of times, is just equal probability everywhere. What if we wan’t to achieve some other final distribution? It turns out we can just fine as long as we are looking for equilibrium states of a particular system, and in fact with a few restrictions on our Markov chain we can get to distributions which otherwise would require an intractable amount of computation.

Generally we’ve been able to say this of our state:

$$ \vec{w}(t + 1) = \hat{W}\vec{w}(t) $$

The state in the next time step is acquired by applying the transformation matrix to the previous timestep. An equilibrium will have been reached when repeated application of the matrix yields no change. e.g.

$$ \vec{w}(t = \infty) = \hat{W}\vec{w}(t = \infty) $$

For our Markov process to reach equilibrium we require some set of states which have no net flow of probability. I’ll draw this out first:

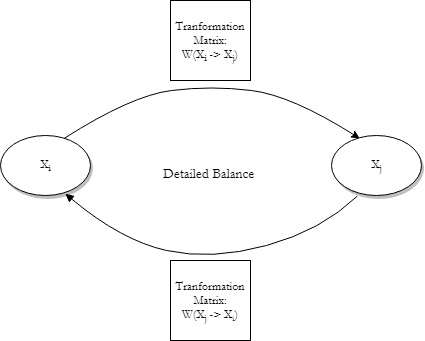
In this cycle of states, which could have easily included more than two states, there is no net flow of probability (or whatever it is your states are measuring!) between any pair of states. You might think of this as the equivalent of some chemical equilibrium in a reaction. This is the detailed balance condition that we want to impose on our process. Another way of describing this would be to say that a particular Markov chain is reversible. 

Writing this out:

$$W(j \rightarrow i)w_j = W(i \rightarrow j)w_i$$

or in the form of a ratio as we will use it:

$$\frac{W(j \rightarrow i)}{W(i \rightarrow j)} = \frac{w_i}{w_j}$$

Again, for any state $i$, to and from any other state $j$.

An example application to the Boltzmann Distribution using the Metropolis-Hastings algorithm

To demonstrate the use of detailed balance in a markov process we can apply the concepts to generate the Boltzmann distribution. The Boltzmann distribution describes the probability of finding a microstate of particles (classically of some gas) with a certain energy $E_i$. It looks like:

$$ w_i = \frac{e^{- \beta(E_i)}}{Z} $$

The states that we are dealing with now are much larger and more complex than the one dimensional single particle. Now we can think of some large distribution of particles in three dimensions, with each possible configuration of particles (within some discretization scheme) making up our explorable “state space”.

$Z$, the partition function, is a normalization coefficient which is the sum of all probabilities across all possible microstates of the system. There are essentially an infinite number of microstates for these systems so brute force population of the distribution via Monte Carlo would be pretty ineffective. However, we know the equilibrium will satisfy the detail balance condition, and so we can select for random movements between states which maintain the detail balance ratio which we described in the previous section. Doing so will bring us to the “solved” equilibrium state without ever having to explicitly integrate over all possible states.

What i’m describing is the acceptance criteria used in the Metropolis algorithm. Given that a Markov process must satisfy a detail balance ratio, for the Boltzmann distribution this means:

$$ \frac{w_i}{w_j} = e^{- \beta(E_i - E_j)} $$

And so, when applying randomized transitions to the state, we want our acceptance rate to conform to this ratio. This “guides” our state transitions towards the equilibrium described by Boltzmann.

So if we make random moves among the particles in the system, and accept/deny those moves based on the criteria:

$$ \frac{A(j \rightarrow i)}{A(i \rightarrow j)} = e^{- \beta(E_i - E_j)} $$

Where $A$ is an acceptance rate for the move between states $i$ and $j$.

We know systems in equilibrium will inhabit the lowest energy states available to them, and so a simple test would be to only accept random state changes which lower the energy. This would give give us solutions, but would get stuck in any local minima which exist in our state space, generally speaking. This is another way of saying that such a simple acceptance criteria would violate ergodicity. Even given an infinite amount of computing time, we would not explore all available states and therefore never be sure that we had found the correct solution rather than a local minimum.

To make our Markov chain abide by this ergodic constraint we must accept moves which do not lower the energy of the state as well, but with a probability which corresponds to the ratio described by the detail balance condition. Detail balance gives us the proper form of the equilibrium distribution, ergodicity ensures that the chain does not get stuck forming that distribution in a local minima. That sums up the Metropolis algorithm, which reads:

$$ A(j \rightarrow i) = \begin{cases} e^{- \beta(E_i - E_j)} & E_i - E_j > 0 \\ 1 & \text{otherwise} \end{cases} $$

To summarize, the Metropolis algorithm is an implementation of a Markov chain which abides by certain constraints such as detailed balance. The detail balance condition one comes up with determines the equilibrium state the chain trends towards, and you can use such a condition to find distributions which would have been intractable by brute force integration or Monte Carlo sampling.

Keep in mind that this is just one sample application. You can see an application of the Metropolis algorithm in my follow up post on the Quantum Variational Monte Carlo

References